ХИМИЧЕСКИЙ ДИЗАЙН

(ОТДЕЛЬНЫЙ ОТТИСК)

МЕТАХИМИЯ

ДИЗАЙНА

РЕФЛЕКСИИ

НАУКОМЕТРИИ

И ЭВЕНТОЛОГИИ

Chem.Lab.NCD

Новосибирск 2012

 

 

 

 

МАТЕРИАЛЫ

 

 

МЕЖДУНАРОДНОЙ АКАДЕМИИ

ЦЕНТРА  НООСФЕРНОЙ ЗАЩИТЫ

И ежегодники "Химический Дизайн"

(1998-2010гг) смотри на сайтах:

 http://squps.wmsite.ru/

 http://sak1.wmsite.ru/

http://kutol.narod.ru/webd.htm

http://kristall.lan.krasu.ru/Science/journals.html

 

 

 

 

 

 

 

 

 

 

 

 Парадигма метахимии золотого сечения

как история событий Ноосферы

 С.А.Кутолин,

профессор, доктор химических наук,

академик  МАН ЦНЗ и РАТ.

   Новосибирск, Россия

 РЕФЕРАТ:Впервые обнаружено, что временная структура исторических событий (глобальный цикл исторических событий Ноосферы, временные тренды  истории России, исторические циклы развития государственности различных этносов в границах общего периода Ноосферы) есть аналити-ческая функция  числовых последовательностей  Люка, Фибоначчи  с коэффициентами корреляции модели свыше 70%. Установлено, что «фрактальная размерность D” есть отношение (последующего к преды-дущему) чисел Люка , Фибоначчи, т.е. «золотое сечение». Тем самым природа исторических циклов событий есть «парадигма золотого сечения Ноосферы», как когнитивность в инвариантном Мире событий.

 

 Введение

   В предыдущей статье рассматривался  временной тренд 1812-2012гг с шагом 20лет. Результаты этого исследования привели к примечательным выводам с позиции метахимической парадигмы рефлексии[1]. Метахи-мический инструментарий позволил выявить алгоритм исчисления временного тренда в рамках 1812-2012гг с шагом 20 лет и кооффициентом корреляции модели практически равным единице. Аргументами такого тренда являются числовые последовательности типа Люка , Фибоначчи и флуктуации, вызываемые, скорее всего, разными типами стратификации событий, которые могут рассматриваться и как фрактальные временные ряды стратификации разных типов событий. Причины возникновения функциональных зависимостей, в отношении которых при больших коэффициентов корреляции модели ( ккм ) имеется аналитическая связь с аргументами числовых последовательностей  Люка, Фибоначчи  есть результат безэнтропийного проявления  «золотого сече-ния». Результаты анализа метахимического опыта позволяют дискрими-нировать категории: «истины – истинности», «опыта – опытности», реалии замкнутости времени на примере фактов и иллюзии в «профессиональном образе мира»  как мира инвариантного. В статье не высказывалось никаких соображений относительно исторической привязки рассматриваемого временного тренда к конкретике исторических событий и тем более истории этноса и цивилизаций. Однако полученные результаты свидетельствовали о том, что расмотрение указанного метода как парадигмы метахимии золотого сечения на примере Ноосферы могло бы послужить самостоятельной задачей изучения временного тренда и для  истории, этноса и цивилизации Мира.    Мира как инвариантности, где метахимическая парадигма рефлексии[2] и есть «золотая парадигма Ноосферы», порождающая «профессиональный образ мира по А.Н.Леонтьеву».

Матричной канвой для проведения указанного исследования могли служить материалы, полученные в исследованиях временной структуры исторических событий, полученных в работе[3], где, в частности, разумно аргументировалось, что «чисто статистический подход к историческим событиям» не состоятелен, поскольку сам  исторический процесс развития человечества, т.е. Ноосферы, будучи наделён «соотвествующей мерой», позволяет различать эти процессы как процессы синэргетические, т.е. обладающие иерархией аналогии в историческом развитии. При этом авторы даже рассмотрели фрактальные временные ряды продолжитель-ности исторического развития N(m) ячеек с общей аппроксимацией  исторического явления как функции «фрактальной размерности D”:

N(m) = C m^-D , где  D= 1,47 – 1,59 для разных стран от Франции до Англии, Германии, Китая, России.

 Действительно, ведь Истина, Истинность и Факт в духе Гёделя – Тарского недвусмысленно доказывают на примере «Антиномии Лжеца», что алгоритмируемые законы непротиворечивы, а не имеющие алгоритма являют собой «формы открытий», в языковой канве которых всегда имеет место противоречие как «антиномия Лжеца». Вот почему метахимия в своём принципе иерархии аналогии или прямого подобия занимается поисками в «золотой парадигме Ноосферы» аналитических решений проблемных ситуаций, где искомая функция описывается аргументами, в качестве  которых используются числа, например, Люка и Фибоначчи, явлениями флуктуации как противоречиями (антиномиями) в смысловых связях (парадигмах) по существу Истины (как предмета анализа в алгоритме) и Истинности (как результата флуктуации, т.е. действия, динамики стратификации в самых различных ёё формах), что может служить примером описания ситуации  в том числе и фрактальными временными рядами, что позволит в дальнейшем, разъяснить смысл фрактальной размерности D, причины её образования в парадигме метахимии «золотого сечения Ноосферы».

Выбор метода анализа, основные посылки

 и результаты   моделирования

 1.Модель исторических периодов Ноосферы. Пусть имеем в качестве аргументов некоторого глобального цикла исторического временного тренда Числа Фибоначчи и Люка u_i  и u_i-1 от i=1¸10, заданнные рядом в форме таблицы1:

Табл1.Числа Фибоначчи и Люка u_i  и u_i-1 от i=1¸10

 

 

а сам глобальный исторический тренд как форму длительности периода (Y_табл.)будем рассматривать с привязкой к общей шкале времени с её крат-кой характеристикой так, как истрический инвариантный образ Мира, используя  в качестве матрицы специально «отсканированную» таблицу работы [3], полагая, что алгоритм такого поиска вполне возможно лежит в форме   простых инвариантных соотношений соотношений регрессии типа Y_расч. =F( Fiba, Td), так что числа Фибиначчи и Люка в линейной регресии есть аргументы функции в форме x_i (Td ,Fibi).

 

 

 

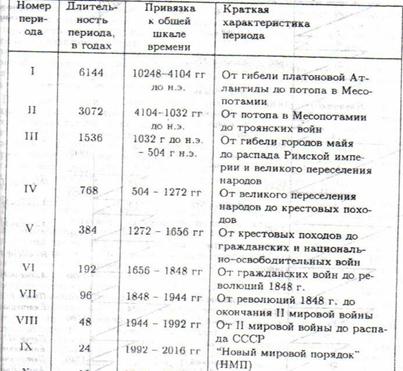
 Тем самым область поиска есть:

где аргументы x_i , величины переменных коэффициентов a_i получаются в результате расчетов, как и постоянный коэффициент (В) модели линейной или квадратичной регрессии. Коэффициент корреляции такой модели (ккм)должен быть достаточно высок, чтобы говорить о функциональной зависимости между табличной величиной Y_табл и расчетным значением этой величины, чтобы принять, что величина D = Y_табл - Y_расч есть величина случайная. В противном случае, модельно – статистическое описание превращается в модельно - эвристическое описание с флуктуацией   стратификации, включение которой в форме величин D в статистическую модель  повышает существенным образом ккм, или по [3] представляет собой фрактальный временной ряд длительности исторического периода. Фактически это означает, что модельно – эвристическое описание сводится к отысканию функции вида:

Y_табл = Y_расч ± Y_сред × F_{распределения} = Y_расч ± D

Полученная модель, во – первых, устанавливает необходимые и достаточные   факторы, влияющие  на коэффициент корреляции модели путём включения или исключения таковых, эвристическая же доминанта, во – вторых, иллюстрирует факт влияния интегральной системы  флуктуакции  какого – то вида стратификации, мера которой определяется величиной Y_сред × F_{распределения} , где среднее значение Y_сред устанавливается самой программой ChemLehr поиска алгоритма.

Исходная матрица regres4.dat (I-IX номер периода) имела вид (длительность периода  6144 в годах):

 

no,np,ny,lo,vread,vprint,znach,psigma

 

 

 

PACЧET ПO ПPOГPAMME < ChemLehr >

  ЧИCЛO PEAЛИЗAЦИЙ                    9

  ЧИCЛO ПAPAMETPOB                    5

  PEЗУЛЬTИPУЮЩИЙ ПAPAMETP             5

  BAPИAHT ПEЧATИ                      2

  KOЭФФИЦИEHT ЗHAЧИMOCTИ           1.00

  KOЭФФИЦИEHT УДAЛEHИЯ PEAЛИЗAЦИЙ   3.0

     CTPOИTCЯ KBAДPATИЧHAЯ MOДEЛЬ

  LX(J)

      0 0 2 2 0

  NOB(I)

      0 1 1 1 1 1 1 1 1

  LP(J)

      1 0 0 0 0

 

          TAБЛИЦA ПEPEKOДИPOBKИ ПAPAMETPA    1

 

    ИC-XOДHOE ЗHAЧEHИE X     HOBOE ЗHAЧEHИE X

 

                 1.00           *********

                 2.00           *********

                 3.00           *********

                 4.00           768.00000

                 5.00           384.00000

                 6.00           192.00000

                 7.00            96.00000

                 8.00            48.00000

                 9.00            24.00000

 

  CP.ЗHAЧEHИE Y                        765.0000000

  ДИCПEPCИЯ Y                      1128703.0000000

  CP.OTKЛOHEHИE Y                     1062.4040000

 

  CPEДHИE ЗHAЧEHИЯ X

     1  765.00000     2    6.45550     3   24.37500     4   10.87500

     5  765.00000

 

  KOЛИЧECTBO ПAPAMETPOB,BKЛЮЧEHHЫX B MOДEЛЬ    2

     ПAPAMETP   3     CTEПEHЬ  1     KOЭФФИЦИEHT     1291.91200

     ПAPAMETP   4     CTEПEHЬ  1     KOЭФФИЦИEHT    -2937.36300

  CBOБOДHЫЙ ЧЛEH УPABHEHИЯ            1218.4610000

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ      442127.5000000

  CPEДHИЙ MOДУЛЬ OШИБKИ                607.5828000

  HECMEЩEHHAЯ OЦEHKA OCTATOЧHOЙ ДИCПEPCИИ                 707403.1   

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ HA KOHTPОЛЬНОЙ BЫБOPKE     .0000000   

  KOЭФФИЦИEHT KOPPEЛЯЦИИ MOДEЛИ  (ккм=74,3%)           .7431877

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM ИCKЛЮЧEHИЯ

              3  49.0    4  51.0

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM BKЛЮЧEHИЯ

              3  49.0    4  51.0

 

Величины no,np,ny,lo,vread,vprint,znach,psigma означают  - число иссле-дуемых объектов, аргументов, искомый признак (5 =Y_табл), ищется линейная или квадратичная зависимость, укороченный (расширенный) вариант печати, коэффициент значимости, коэффициент удаления реализации. 

Поразительным результатом расчета является сам факт высокого коэффициента корреляции модели (ккм=74%) между длительностью периодов(I-IX) и величинами аргументов ряда Люка (аргумент3) и Фибоначчи (аргумент4), при этом вклад включённых параметров, расчитанных методом включения - исключения равновелики приблизи-тельно в процентном отношении. Более того, удивительным является следующий факт(regres5.rez): достаточно ограничиться только I - VIII периодами глобального цикла (12288лет), приводимыми в сканированной таблице вплоть до 1944-1992гг как коэффициент корреляции модели искомой функции оказывается равным ккм = 83%, при приблизительно одинаковом значении вклада в модель чисел Люка и Фибоначчи (52-49%):

 

PACЧET ПO ПPOГPAMME < ChemLehr >

 

  ЧИCЛO PEAЛИЗAЦИЙ                    8

  ЧИCЛO ПAPAMETPOB                    5

  PEЗУЛЬTИPУЮЩИЙ ПAPAMETP             5

  BAPИAHT ПEЧATИ                      2

  KOЭФФИЦИEHT ЗHAЧИMOCTИ           1.00

  KOЭФФИЦИEHT УДAЛEHИЯ PEAЛИЗAЦИЙ   3.0

     CTPOИTCЯ KBAДPATИЧHAЯ MOДEЛЬ

  LX(J)

      0 0 2 2 0

  NOB(I)

      0 0 1 1 1 1 1 1

  LP(J)

      1 0 0 0 0

          TAБЛИЦA ПEPEKOДИPOBKИ ПAPAMETPA    1

    ИC-XOДHOE ЗHAЧEHИE X     HOBOE ЗHAЧEHИE X

 

                 1.00           *********

                 2.00           *********

                 3.00           *********

                 4.00           768.00000

                 5.00           384.00000

                 6.00           192.00000

                 7.00            96.00000

                 8.00            48.00000

 

  CP.ЗHAЧEHИE Y                        504.0000000

  ДИCПEPCИЯ Y                       324172.8000000

  CP.OTKЛOHEHИE Y                      569.3618000

  CPEДHИE ЗHAЧEHИЯ X

     1  504.00000     2   15.38983     3   19.33333     4    8.66667

     5  504.00000

  KOЛИЧECTBO ПAPAMETPOB,BKЛЮЧEHHЫX B MOДEЛЬ    2

     ПAPAMETP   3     CTEПEHЬ  1     KOЭФФИЦИEHT     -860.89470

     ПAPAMETP   4     CTEПEHЬ  1     KOЭФФИЦИEHT     1874.76300

  CBOБOДHЫЙ ЧЛEH УPABHEHИЯ             900.0143000

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ       84000.0500000

  CPEДHИЙ MOДУЛЬ OШИБKИ                280.0002000

  HECMEЩEHHAЯ OЦEHKA OCTATOЧHOЙ ДИCПEPCИИ                 167999.9   

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ HA KOHTPОЛЬНОЙ BЫБOPKE     .0000000   

  KOЭФФИЦИEHT KOPPEЛЯЦИИ MOДEЛИ (ккм=83%)      .8300931

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM ИCKЛЮЧEHИЯ

              3  51.5    4  48.5

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM BKЛЮЧEHИЯ

              3  51.5    4  48.5

Тем самым моделирование глобального цикла в рамках громадного периода его длительности вплоть до 2016г позволяет убедиться в инвариантности Мира исторических событий, рассмотренные циклы которых есть функциональная зависимость от чисел Люка и Фибоначчи, что свидетельствует о явной смысловой связи (парадигме) между характеристиками исторических периодов Ноосферы и числовыми последовательностями Люка, Фибоначчи, в которых отношение каждого последующего члена ряда к предыдущему есть «золотое сечение». Тем самым иллюстрируется «парадигма золотого сечения Ноосферы», привязанная к общей шкале исторического времени существования самой Ноосферы.

2.Модель исторических циклов России. Воспользуемся сканированными материалами работы [3] по описанию исторических циклов России. И применим к описанию этих циклов для выявления «парадигмы золотого сечения Ноосферы» методику моделирования исторических циклов России как функции числовых последовательностей Люка и Фибоначчи.

 

2а.Моделирование парадигмы «золотого сечения Ноосферы» Руси Киевской (573-1341гг). Результаты моделирования по изложенной выше методике имеют следующие  результаты моделирования:

 

 

PACЧET ПO ПPOГPAMME < ChemLehr >

  ЧИCЛO PEAЛИЗAЦИЙ                    9

  ЧИCЛO ПAPAMETPOB                    5

  PEЗУЛЬTИPУЮЩИЙ ПAPAMETP             5

  BAPИAHT ПEЧATИ                      2

  KOЭФФИЦИEHT ЗHAЧИMOCTИ           1.00

  KOЭФФИЦИEHT УДAЛEHИЯ PEAЛИЗAЦИЙ   3.0

     CTPOИTCЯ KBAДPATИЧHAЯ MOДEЛЬ

  LX(J)

      0 0 2 2 0

  NOB(I)

      0 1 1 1 1 1 1 1 1

  LP(J)

      1 0 0 0 0

          TAБЛИЦA ПEPEKOДИPOBKИ ПAPAMETPA    1

 

    ИC-XOДHOE ЗHAЧEHИE X     HOBOE ЗHAЧEHИE X

 

                 1.00           573.00000

                 2.00           669.00000

                 3.00           765.00000

                 4.00           861.00000

                 5.00           957.00000

                 6.00           *********

                 7.00           *********

                 8.00           *********

                 9.00           *********

  CP.ЗHAЧEHИE Y                       1005.0000000

  ДИCПEPCИЯ Y                        55296.0000000

  CP.OTKЛOHEHИE Y                      235.1510000

  CPEДHИE ЗHAЧEHИЯ X

     1 1005.00000     2 -382.37500     3   24.37500     4   10.87500

     5 1005.00000

  KOЛИЧECTBO ПAPAMETPOB,BKЛЮЧEHHЫX B MOДEЛЬ    2

     ПAPAMETP   3     CTEПEHЬ  1     KOЭФФИЦИEHT      -92.57143

     ПAPAMETP   4     CTEПEHЬ  1     KOЭФФИЦИEHT      225.14290

  CBOБOДHЫЙ ЧЛEH УPABHEHИЯ             812.9999000

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ        7213.7130000

  CPEДHИЙ MOДУЛЬ OШИБKИ                 77.7143100

  HECMEЩEHHAЯ OЦEHKA OCTATOЧHOЙ ДИCПEPCИИ                 11541.95   

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ HA KOHTPОЛЬНОЙ BЫБOPKE     .0000000   

  KOЭФФИЦИEHT KOPPEЛЯЦИИ MOДEЛИ(ккм=92,2%)           .9224462

 

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM ИCKЛЮЧEHИЯ

              3  45.7    4  54.3

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM BKЛЮЧEHИЯ

              3  45.7    4  54.3

Результаты моделирования парадигмы «золотого сечения Ноосферы исторических циклов Киевской Руси отличаются высоким коэффициентов корреляции модели – 92,2%, а вклад включенных параметров числовых последовательностей Люка и Фибоначчи, расчитанные методом включения – исключения равны 46-54%. Этот результат сам по себе удивителен тем, что циклическая зависимость между историческими периодами прослеживается с парктически функциональным коэффициентом корреляции модели.

 

2б.Моделирование парадигмы «золотого сечения Ноосферы» Великой Московской Руси(1341-1725гг). Результаты этого моделирования не менее впечатляющи , поскольку коэффициент корреляции модели (ккм=92,2%)  свидетелсьтвует не только о высокой функциональной зависимости историчесих цикло этого времени от последовательностей Люка и Фибоначчи,, видимо, и о достаточно высокой точности датировки данного исторического цикла развития Московии. В этом смысле честь и хвала покойному академику Рыбаковы, чьи специальным работы в этой области побудили автора настоящего исследования «серьёзно почитывать» работы академика  по названному историческому периоду.

 

PACЧET ПO ПPOГPAMME <ChemLehr>

 

  ЧИCЛO PEAЛИЗAЦИЙ                    9

  ЧИCЛO ПAPAMETPOB                    5

  PEЗУЛЬTИPУЮЩИЙ ПAPAMETP             5

  BAPИAHT ПEЧATИ                      2

  KOЭФФИЦИEHT ЗHAЧИMOCTИ           1.00

  KOЭФФИЦИEHT УДAЛEHИЯ PEAЛИЗAЦИЙ   3.0

     CTPOИTCЯ KBAДPATИЧHAЯ MOДEЛЬ

  LX(J)

      0 0 2 2 0

  NOB(I)

      0 1 1 1 1 1 1 1 1

  LP(J)

      1 0 0 0 0

          TAБЛИЦA ПEPEKOДИPOBKИ ПAPAMETPA    1

    ИC-XOДHOE ЗHAЧEHИE X     HOBOE ЗHAЧEHИE X

 

                 1.00           *********

                 2.00           *********

                 3.00           *********

                 4.00           *********

                 5.00           *********

                 6.00           *********

                 7.00           *********

                 8.00           *********

                 9.00           *********

  CP.ЗHAЧEHИE Y                       1557.0000000

  ДИCПEPCИЯ Y                        13824.0000000

  CP.OTKЛOHEHИE Y                      117.5755000

  CPEДHИE ЗHAЧEHИЯ X

     1 1557.00000     2 -382.37500     3   24.37500     4   10.87500

     5 1557.00000

  KOЛИЧECTBO ПAPAMETPOB,BKЛЮЧEHHЫX B MOДEЛЬ    2

     ПAPAMETP   3     CTEПEHЬ  1     KOЭФФИЦИEHT      -46.28571

     ПAPAMETP   4     CTEПEHЬ  1     KOЭФФИЦИEHT      112.57140

  CBOБOДHЫЙ ЧЛEH УPABHEHИЯ            1461.0000000

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ        1803.4270000

  CPEДHИЙ MOДУЛЬ OШИБKИ                 38.8571000

  HECMEЩEHHAЯ OЦEHKA OCTATOЧHOЙ ДИCПEPCИИ                 2885.489   

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ HA KOHTPОЛЬНОЙ BЫБOPKE     .0000000   

  KOЭФФИЦИEHT KOPPEЛЯЦИИ MOДEЛИ (ккм=92,2%)  .9224462

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM ИCKЛЮЧEHИЯ

              3  45.7    4  54.3

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM BKЛЮЧEHИЯ

              3  45.7    4  54.3

 

2в.Моделирование парадигмы «золотого сечения Ноосферы» Всероссий-ской империи(1725-1917гг). При фукционально значимом коээфициенте корреляции модели (ккм= 92%) и вкладе включенных параметров последовательностей Люка и Фибоначчи 45-54% следует обратить внимание на то, что получаемые в модели оценки дисперсии, ошибки, свободоных членов уравнений не идентичны между собой, а потому сами исторические циклы имеют явно индивидуальный «характер» исторического «действа».

 

PACЧET ПO ПPOГPAMME <ChemLehr>

  ЧИCЛO PEAЛИЗAЦИЙ                    9

  ЧИCЛO ПAPAMETPOB                    5

  PEЗУЛЬTИPУЮЩИЙ ПAPAMETP   5

  BAPИAHT ПEЧATИ                      2

  KOЭФФИЦИEHT ЗHAЧИMOCTИ           1.00

  KOЭФФИЦИEHT УДAЛEHИЯ PEAЛИЗAЦИЙ   3.0

     CTPOИTCЯ KBAДPATИЧHAЯ MOДEЛЬ

  LX(J)

      0 0 2 2 0

  NOB(I)

      0 1 1 1 1 1 1 1 1

  LP(J)

      1 0 0 0 0

 

          TAБЛИЦA ПEPEKOДИPOBKИ ПAPAMETPA    1

    ИC-XOДHOE ЗHAЧEHИE X     HOBOE ЗHAЧEHИE X

                 1.00           *********

                 2.00           *********

                 3.00           *********

                 4.00           *********

                 5.00           *********

                 6.00           *********

                 7.00           *********

                 8.00           *********

                 9.00           *********

 

  CP.ЗHAЧEHИE Y               1833.0000000

  ДИCПEPCИЯ Y                         3456.0000000

  CP.OTKЛOHEHИE Y                       58.7877500

  CPEДHИE ЗHAЧEHИЯ X

     1 1833.00000     2 -382.37500     3   24.37500     4   10.87500

     5 1833.00000

  KOЛИЧECTBO ПAPAMETPOB,BKЛЮЧEHHЫX B MOДEЛЬ    2

     ПAPAMETP   3     CTEПEHЬ  1     KOЭФФИЦИEHT      -23.14286

     ПAPAMETP   4     CTEПEHЬ  1     KOЭФФИЦИEHT       56.28571

  CBOБOДHЫЙ ЧЛEH УPABHEHИЯ            1785.0000000

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ         450.8569000

  CPEДHИЙ MOДУЛЬ OШИБKИ                 19.4285600

  HECMEЩEHHAЯ OЦEHKA OCTATOЧHOЙ ДИCПEPCИИ                 721.3712   

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ HA KOHTPОЛЬНОЙ BЫБOPKE     .0000000   

  KOЭФФИЦИEHT KOPPEЛЯЦИИ MOДEЛИ  (ккм=(92%)    .9224463

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM ИCKЛЮЧEHИЯ

              3  45.7    4  54.3

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM BKЛЮЧEHИЯ

              3  45.7    4  54.3

 

2г.Моделирование парадигмы «золотого сечения Ноосферы» Советской Социалистической Руси(1917-2013гг). При сравнении результатов моделирования исторических циклов России выделяется какая – то особая внутренняя связь между различными историческими циклами России, эта связь имеет какой – то особый внутренний характер, который улавли-вается пока лишь в числовой близости в процентном отношении вклада включенных парамтров последовательностей Лука и Фибоначчи. Появля-ется такое ощущение при сравнении результатов моделирования, что не только циклы исторических временных трендов связаны между собой «парадигмой золотого сечения Ноосферы», но и внутри циклов имеются не менее сильные связи пока в явном виде не выявленные в модели каких – то внутренних  ещё повидимому не включенных в модель  аргументов, несущих свою в не явном виде смысловую нагрузку.

 

 

PACЧET ПO ПPOГPAMME <ChemLehr>

  ЧИCЛO PEAЛИЗAЦИЙ                    9

  ЧИCЛO ПAPAMETPOB                    5

  PEЗУЛЬTИPУЮЩИЙ ПAPAMETP   5

  BAPИAHT ПEЧATИ                      2

  KOЭФФИЦИEHT ЗHAЧИMOCTИ           1.00

  KOЭФФИЦИEHT УДAЛEHИЯ PEAЛИЗAЦИЙ   3.0

     CTPOИTCЯ KBAДPATИЧHAЯ MOДEЛЬ

  LX(J)

      0 0 2 2 0

  NOB(I)

      0 1 1 1 1 1 1 1 1

  LP(J)

      1 0 0 0 0

          TAБЛИЦA ПEPEKOДИPOBKИ ПAPAMETPA    1

    ИC-XOДHOE ЗHAЧEHИE X     HOBOE ЗHAЧEHИE X

                 1.00           *********

                 2.00           *********

                 3.00           *********

                 4.00           *********

                 5.00           *********

                 6.00           *********

                 7.00           *********

                 8.00           *********

                 9.00           *********

 

  CP.ЗHAЧEHИE Y                       1971.0000000

  ДИCПEPCИЯ Y                          864.0000000

  CP.OTKЛOHEHИE Y                       29.3938800

  CPEДHИE ЗHAЧEHИЯ X

     1 1971.00000     2 -382.37500     3   24.37500     4   10.87500

     5 1971.00000

  KOЛИЧECTBO ПAPAMETPOB,BKЛЮЧEHHЫX B MOДEЛЬ    2

     ПAPAMETP   3     CTEПEHЬ  1     KOЭФФИЦИEHT      -11.57143

     ПAPAMETP   4     CTEПEHЬ  1     KOЭФФИЦИEHT       28.14286

  CBOБOДHЫЙ ЧЛEH УPABHEHИЯ            1947.0000000

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ         112.7147000

  CPEДHИЙ MOДУЛЬ OШИБKИ                  9.7143400

  HECMEЩEHHAЯ OЦEHKA OCTATOЧHOЙ ДИCПEPCИИ                 180.3428   

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ HA KOHTPОЛЬНОЙ BЫБOPKE     .0000000   

  KOЭФФИЦИEHT KOPPEЛЯЦИИ MOДEЛИ  (ккм=92%)         .9224459

 

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM ИCKЛЮЧEHИЯ

              3  45.7    4  54.3

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM BKЛЮЧEHИЯ

              3  45.7    4  54.3

 

Именно этот момент существования каких – то в модели не выявленных связей, но достаточно существенных, видимо, для исторического пони-мания циклоидного развития истории, в данном случае  России, именно такой вывод напрашивается в результате сравнений исторических циклов развития Руси – России, о чём недвусмысленно свидетельствуют  результаты этого моделирования исторических циклов по «образу и подобию» модельно – статистических параметров, которые, кстати, явно говорят не в пользу чисто статистических апроксимаций исторических событий без учета «парадигмы золотого сечения Ноосферы» как метахимического образа инвариантности Мира в целом.Однако полученные результаты моделирования могут служить основанием для их осмысливания путём постановки эвристического задания, в котором следует учитывать не только вклад включенных параметров последовательностей Люка и Фибоначчи, но и категорий стратификации образа времени исторических событий, которые достаточно полно обсуждаются в работах Питирима Сорокина[4]. В качестве такой формы стратификации как флюктуации может быть выбрана объективная величина.

Коэффициент корреляции такой модели (ккм)должен быть достаточно высок, чтобы говорить о функциональной зависимости между табличной величиной Y_табл и расчетным значением этой величины, чтобы принять, что величина D = Y_табл - Y_расч есть величина случайная. В противном случае, модельно – статистическое описание превращается в модельно - эвристическое описание с флуктуацией   стратификации, включение которой в форме величин D в статистическую модель  повышает существенным образом ккм. Фактически это означает, что модельно – эвристическое описание сводится к отысканию функции вида:

Y_табл = Y_расч ± Y_сред × F_{распределения} = Y_расч ± D

Полученная модель, во – первых, устанавливает необходимые и достаточные   факторы, влияющие  на коэффициент корреляции модели путём включения или исключения таковых, эвристическая же доминанта, во – вторых, иллюстрирует факт влияния интегральной системы  флуктуакции  какого – то вида стратификации, мера которой определяется величиной Y_сред × F_{распределения} , где среднее значение Y_сред устанавливается самой программой ChemLehr поиска алгоритма. И действительно, если в программу ChemLehr вставить величины Y_сред × F_{распределения,} то полученная матрица regres.dat для моделирование парадигмы «золотого сечения Ноосферы» Советской Социалистической Руси (1917-2013гг) приводит к получению поразительного результата, где практически фрактальность временного ряда сводится к нулю, т.е. идея о флуктуации стратификации исторических событий П.А.Сорокина более чем разумна. Увы, такая идея никогда не подвергалась предлагаемой форме эвристического описания, которая используется в настоящей модели метахимии инвариантных пространств Мира. Результаты же такого компьютерного моделирования следующие:

 

 

PACЧET ПO ПPOГPAMME < ChemLehr >

  ЧИCЛO PEAЛИЗAЦИЙ                    9

  ЧИCЛO ПAPAMETPOB                    5

  PEЗУЛЬTИPУЮЩИЙ ПAPAMETP (Y_табл ) 5

  BAPИAHT ПEЧATИ                      2

  KOЭФФИЦИEHT ЗHAЧИMOCTИ           1.00

  KOЭФФИЦИEHT УДAЛEHИЯ PEAЛИЗAЦИЙ   3.0

     CTPOИTCЯ KBAДPATИЧHAЯ MOДEЛЬ

  LX(J)

      0 2 2 2 0

  NOB(I)

      0 1 1 1 1 1 1 1 1

  LP(J)

      1 0 0 0 0

          TAБЛИЦA ПEPEKOДИPOBKИ ПAPAMETPA    1

    ИC-XOДHOE ЗHAЧEHИE X     HOBOE ЗHAЧEHИE X

                 1.00           *********

                 2.00           *********

                 3.00           *********

                 4.00           *********

                 5.00           *********

                 6.00           *********

                 7.00           *********

                 8.00           *********

                 9.00           *********

  CP.ЗHAЧEHИE Y                       1971.0000000

  ДИCПEPCИЯ Y                          864.0000000

  CP.OTKЛOHEHИE Y                       29.3938800

  CPEДHИE ЗHAЧEHИЯ X

     1 1971.00000     2     .00025     3   24.37500     4   10.87500

     5 1971.00000

  KOЛИЧECTBO ПAPAMETPOB,BKЛЮЧEHHЫX B MOДEЛЬ    3

     ПAPAMETP   2     CTEПEHЬ  1     KOЭФФИЦИEHT        1.00001

     ПAPAMETP   3     CTEПEHЬ  1     KOЭФФИЦИEHT      -11.57184

     ПAPAMETP   4     CTEПEHЬ  1     KOЭФФИЦИEHT       28.14377

  CBOБOДHЫЙ ЧЛEH УPABHEHИЯ            1947.0000000

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ            .0000001

  CPEДHИЙ MOДУЛЬ OШИБKИ                   .0002441

  HECMEЩEHHAЯ OЦEHKA OCTATOЧHOЙ ДИCПEPCИИ                 .1553265E-06

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ HA KOHTPОЛЬНОЙ BЫБOPKE     .0000000      KOЭФФИЦИEHT KOPPEЛЯЦИИ MOДEЛИ          1.0000000

BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM ИCKЛЮЧEHИЯ

             2 (D)   .1    3  45.7 (Td)   4(Fiba)  54.3

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM BKЛЮЧEHИЯ

              2 (D)  49.8    3(Td)     22.9    4 (Fiba)   27.2      

    

 

                          П P O Г H O З  Y_табл

 ----------------------------------------------------------------------

 :   № : Y_табл : Y_расч:       D :     № :  Y_табл : Y_расч :    D:

 ---------------------------------------------------------------------

      1  1917.0  1917.0   -.000        2      1929.0 1929.0    .000

      3  1941.0  1941.0     .000       4      1953.0 1953.0   -.000

      5  1965.0  1965.0    -.000      6     1977.0 1977.0    .000

      7  1989.0  1989.0     .000      8     2001.0  2001.0    .000

      9  2013.0  2013.0    -.000

 

Преимущества модельно – эвристического моделирования в рамках метахимии парадигмы инвариантных пространств Мира золотого сечения Ноосферы очевидны.

 

 

   3.Моделирование парадигмы «золотого сечения Ноосферы» временных трендов исторических циклов развития государственности.

Тем не менее, попытаемся проанализировать временные тренды истории развития государственности различных этносов, используя избранный метод моделирования временного тренда как функции рядов чисел Люка и Фибоначчи. Сканированная матрица и з работы [3] имеет вид:

 

 

 

 

 

 Результаты моделирования приведены ниже и получены с достаточно высоким для анализируемого периода коэффициентом корреляции модели (ккм=74.3%):

 

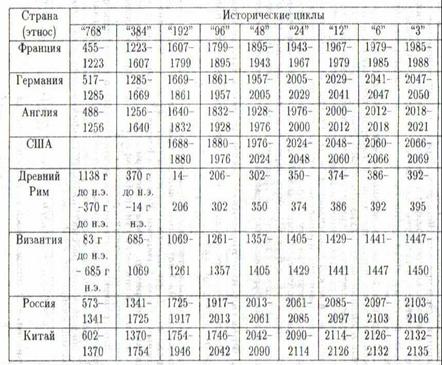
PACЧET ПO ПPOГPAMME <ChemLehr>

  ЧИCЛO PEAЛИЗAЦИЙ                    9

  ЧИCЛO ПAPAMETPOB                    5

  PEЗУЛЬTИPУЮЩИЙ ПAPAMETP             5

  BAPИAHT ПEЧATИ                      2

  KOЭФФИЦИEHT ЗHAЧИMOCTИ           1.00

  KOЭФФИЦИEHT УДAЛEHИЯ PEAЛИЗAЦИЙ   3.0

     CTPOИTCЯ KBAДPATИЧHAЯ MOДEЛЬ

  LX(J)

      0 0 2 2 0

  NOB(I)

      0 1 1 1 1 1 1 1 1

  LP(J)

      1 0 0 0 0

          TAБЛИЦA ПEPEKOДИPOBKИ ПAPAMETPA    1

 

    ИC-XOДHOE ЗHAЧEHИE X     HOBOE ЗHAЧEHИE X

                 1.00           768.00000

                 2.00           384.00000

                 3.00           192.00000

                 4.00            96.00000

                 5.00            48.00000

                 6.00            24.00000

                 7.00            12.00000

                 8.00             6.00000

                 9.00             3.00000

 

 

CP.ЗHAЧEHИE Y                         95.6250000

  ДИCПEPCИЯ Y                        17635.9800000

  CP.OTKЛOHEHИE Y                      132.8005000

  CPEДHИE ЗHAЧEHИЯ X

     1   95.62500     2 -382.37500     3   24.37500     4   10.87500

     5   95.62500

  KOЛИЧECTBO ПAPAMETPOB,BKЛЮЧEHHЫX B MOДEЛЬ    2

     ПAPAMETP   3     CTEПEHЬ  1     KOЭФФИЦИEHT      161.48900

     ПAPAMETP   4     CTEПEHЬ  1     KOЭФФИЦИEHT     -367.17030

  CBOБOДHЫЙ ЧЛEH УPABHEHИЯ             152.3077000

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ        6908.2420000

  CPEДHИЙ MOДУЛЬ OШИБKИ                 75.9478500

  HECMEЩEHHAЯ OЦEHKA OCTATOЧHOЙ ДИCПEPCИИ                 11053.17   

  CPEДHЯЯ OCTATOЧHAЯ ДИCПEPCИЯ HA KOHTPОЛЬНОЙ BЫБOPKE     .0000000   

  KOЭФФИЦИEHT KOPPEЛЯЦИИ MOДEЛИ(ккм=74.3%)           .7431877

 

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM ИCKЛЮЧEHИЯ

              3(Td)  49.0    4(Fiba)  51.0

     BKЛAД BKЛЮЧEHHЫX ПAPAMETPOB,PACCЧИTAHHЫЙ METOДOM BKЛЮЧEHИЯ

             3(Td)    49.0    4(Fiba)   51.0

 

Результаты моделирования временных трендов истории фактически свидетельствуют по всей области исторического анализа развития Ноосферы о фундаментальности найденных соотношений как «парадигмы золотого сечения Ноосферы». Не является исключением и данный случай анализа исторических циклов развития государственности различных этносов в границах рассматриваемого периода, величины которого есть функция числовых последовательностей ряда Люка и Фибоначчи с вкладом включенных параметров 49-51%! Не прибегая больше к анализу  флуктуации стратификации временных трендов истории, воспользуемся ходом анализа таких социальных явлений с использованием фрактальных временных рядов  и соответствующих им дифференциальных уравнений  в том числе и для описания исторических этапов как это было предложено [3] или в последнее время представлено в научной литературе[5] , поскольку циклы в природе естествознания,социологии и экономике достаточно широко обсуждаются в научно – технической литературе[6], а сам автор настоящей работы даже построил теорию неорганического материаловедения, положив в основу несколько иные описания, чем авторы работы [5], например уравнения Фоккера – Планка для прогнозирования новых видов материалов и даже описания цепных процессов синтеза и горения в плазме электрической дуги[7].Всё это говорит о важном свойстве явлений ивариантного Мира как мира когнитивного. Не вдаваясь в подробности описания в том числе и исторических явлений математическими методами, например, как это делал Н.П.Рашевский в своей книге «История глазами математика», просто обратим внимание на конечный результат, апроксимации исторических явлений фрактальной размерностью D в форме[3,5] :

 

N(m) = C m^-D ,

где  D= 1,47 – 1,59 для разных стран от Франции до Англии , Германии, Китая, России. Результат интересен тем в рамках осуществляемого метода моделирования, что смысловая доминанта «фрактальной размерности D» есть ни что иное как отношение чисел Люка (Td) и Фибоначчи (Fiba)  каждого последующего к предыдущему как это следует из таблицы1 настоящей работы. А сам путь модельно – эвристического описания   временных трендов исторических событий Ноосферы впервые доказывает   природу циклов истории как явление «парадигмы золотого сечения Ноосферы» в инвариантном Мире когнитивных событий метахимии.